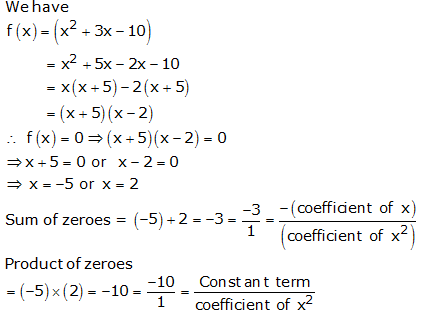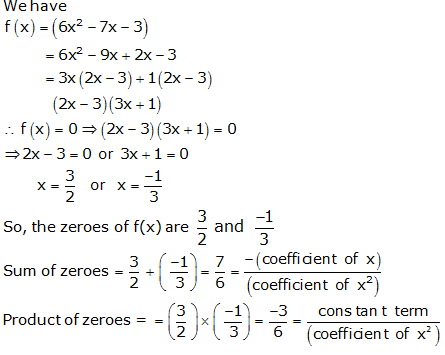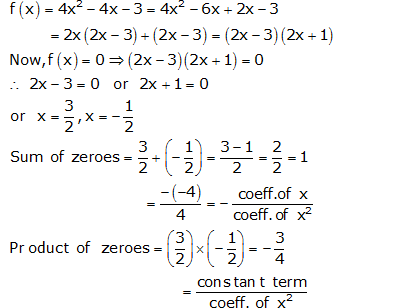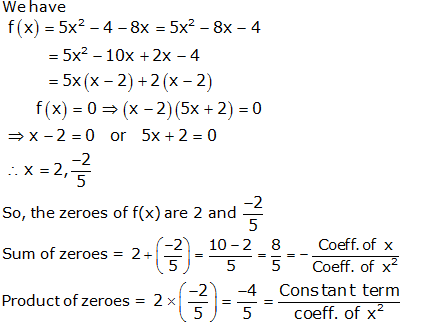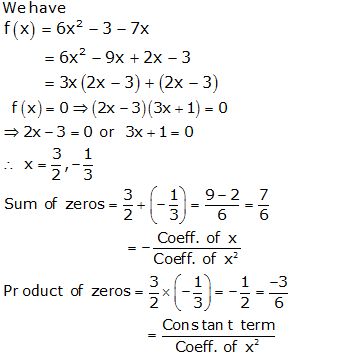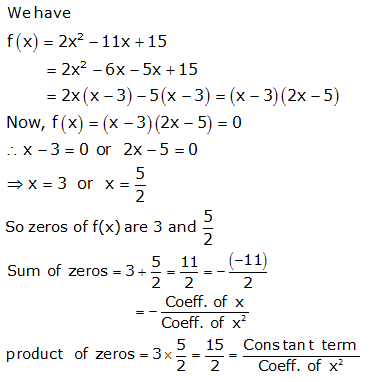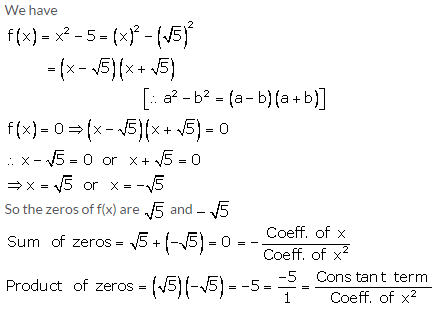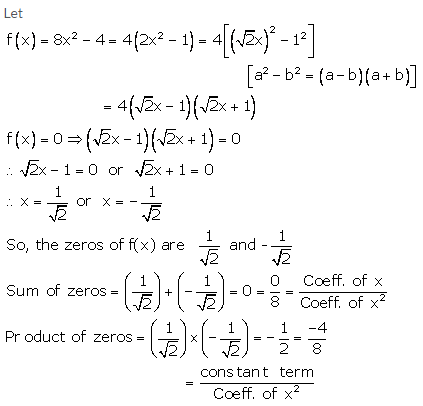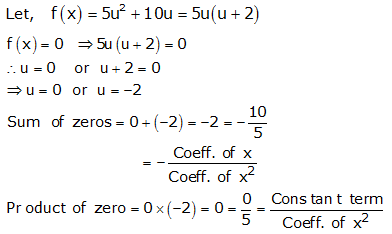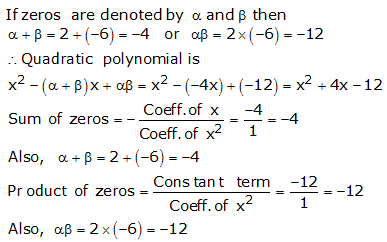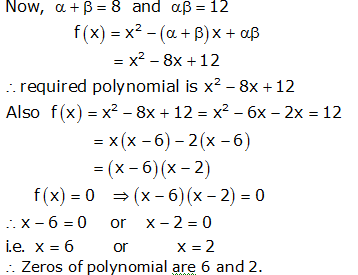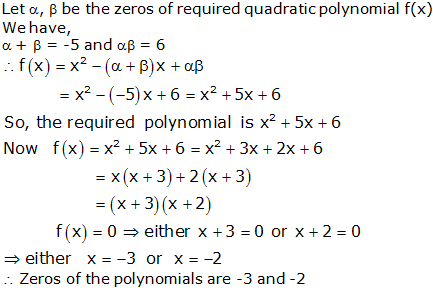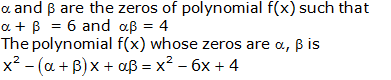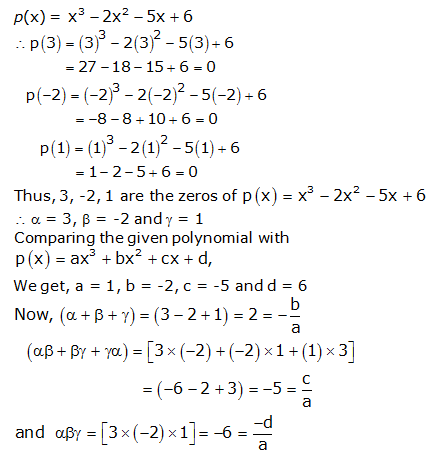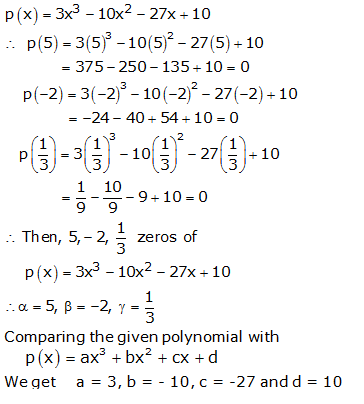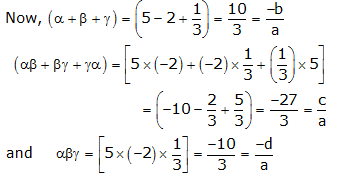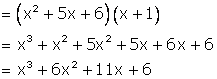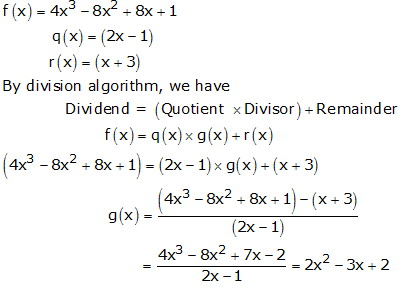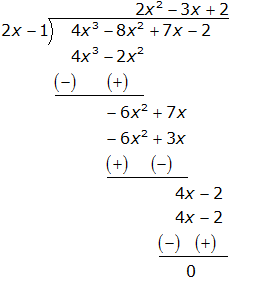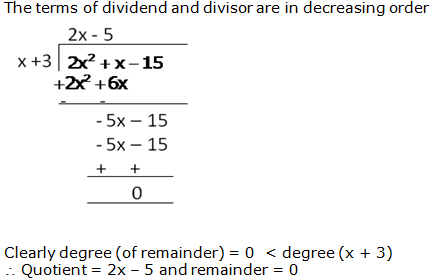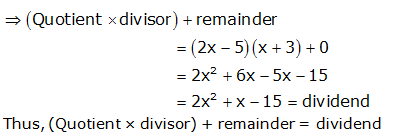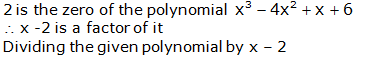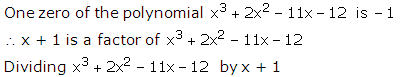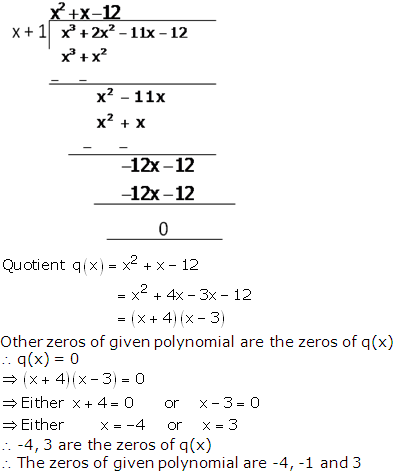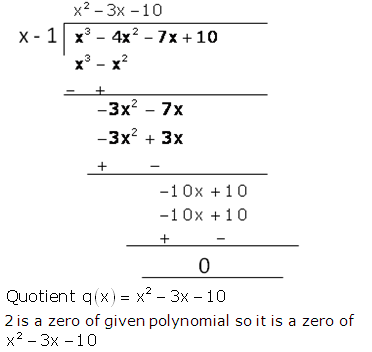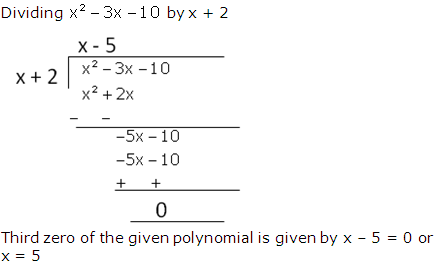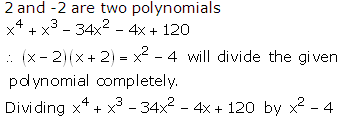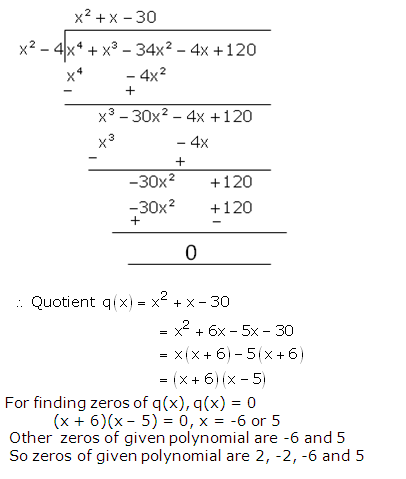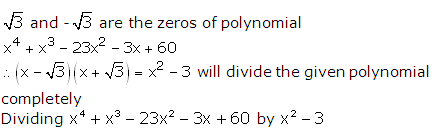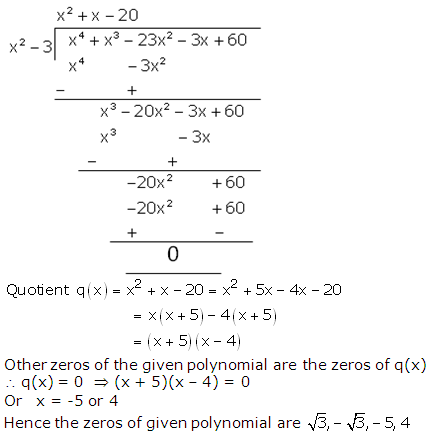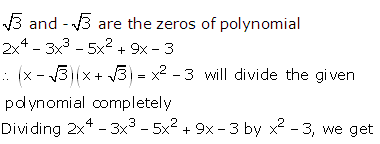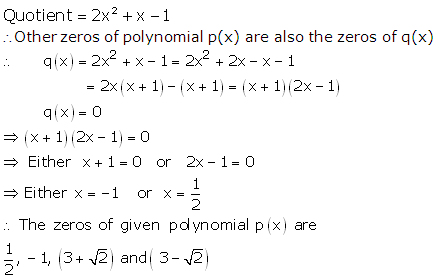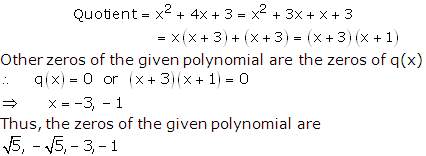RS Aggarwal Solutions Class 10 Maths Chapter 2: If you are looking for a good help book for your Class 10 Maths tests and assignments, then you must refer to the RS Aggarwal Solutions Class 10 Maths. Here you will find step-by-step solutions, prepared by the subject matter experts.
To download the Free PDF of RS Aggarwal Solutions Class 10 Maths Chapter 2, refer to this blog.
Download Free PDF Of RS Aggarwal Solutions Class 10 Maths Chapter 2
Access Solutions Of RS Aggarwal Solutions Class 10 Maths Chapter 2
Exercise 2A
Question 1:
Question 2:
Question 3:
Question 4:
Question 5:
Question 6:
Question 7:
Question 8:
Question 9:
Question 10:
Question 11:
Question 12:
Question 13:
Question 14:
Question 15:
Question 16:
Question 17:
Exercise 2B
Question 1:
Question 2:
Question 3:
Required polynomial = [x – (-2)] [x – (-3)] [x – (-1)]
= (x + 2) (x + 3)(x + 1)
Question 4:
Question 5:
Question 6:
Question 7:
Question 8:
Question 9:
Question 10:
Question 11:
Question 12:
Question 13:
Question 14:
Question 15:
Question 16:
Question 17:
Question 18:
Can I download all exercise solutions of RS Aggarwal Solutions Class 10 Maths Chapter 2 Polynomials?
Yes, in this above article, you can download all exercise solutions of RS Aggarwal Solutions Class 10 Maths Chapter 2 Polynomials.
Are these solutions of RS Aggarwal Solutions Class 10 Maths Chapter 2 Polynomials available for free download?
Yes, solutions of RS Aggarwal Solutions Class 10 Maths Chapter 2 Polynomials are available for free download.
From where can I get the Chapter-wise CBSE Class 10 Maths RS Aggarwal Solutions PDF?
You can refer to the above article to get the Chapter-wise CBSE Class 10 Maths RS Aggarwal Solutions PDF.
Can I download these RS Aggarwal solutions class 10 maths chapter 2 Polynomials on my smartphone?
Yes, you can download solutions of RS Aggarwal Solutions Class 10 Maths Chapter 2 Polynomials on any device.
What are the topics covered under Chapter Polynomials?
Types of Polynomials ie, Linear, Quadratic, Cubic, and Biquadratic Polynomials
Values and Zeros of Polynomials
Relation Between Co-efficient and Zeros of a Polynomial