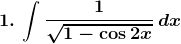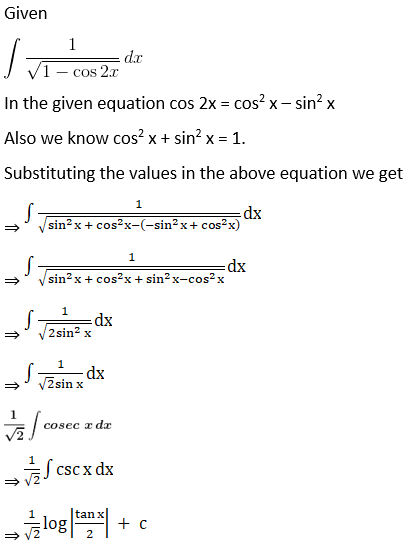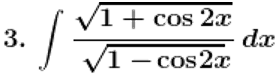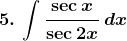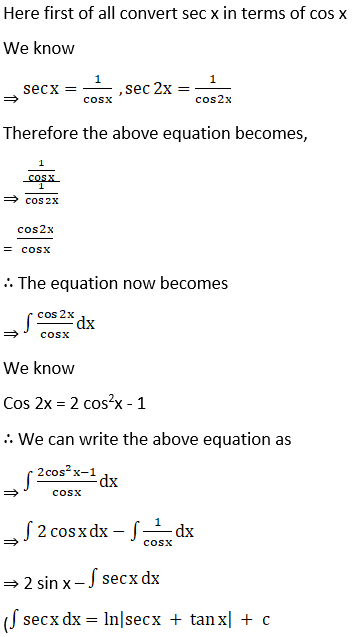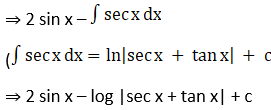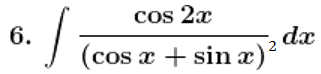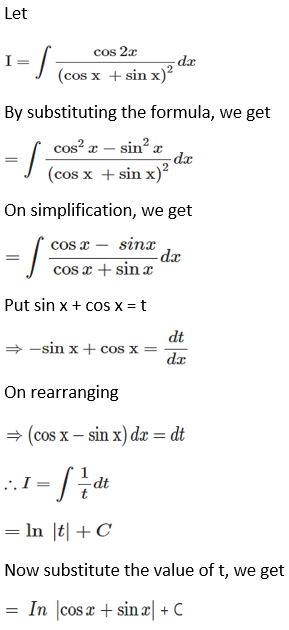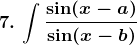RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8: Solutions PDF is an important reference guide to help students score well in the Class 12 exam. By solving exercise problems on a daily basis, students improve their problem-solving and logical thinking skills. This is important for getting better academic grades. The main goal is to help students self-analyze the areas that require the most practice from the exam point of view. With the help of RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8, students can solve exercise problems in a short duration clearly.
Download RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8 PDF:
RD-Sharma-Solutions-Class-12-Maths-Chapter-19-Ex-19.8
Access RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8
Solution:
Solution:
Given,
Solution:
Solution:
Solution:
Therefore,
= cos (b – a)x + sin(b – a) log |sin(x – b)| + c, where c is an arbitrary constant.
RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8: Important Topics From The Chapter
Some of the essential topics covered in this chapter are listed below.
- Definition of primitive or antiderivative
- Definition and meaning of indefinite integral
- Fundamental integration formulae
- Some standard results on integration along with the corollary
- Integration of trigonometric functions
- Integration of exponential functions
- Miscellaneous problems
- Geometrical interpretation of indefinite integral
- Comparison between differentiation and integration
- Methods of integration
- Integration by substitution
- Some standard results
- Evaluation of integrals by using trigonometric substitutions
- Some special integrals
- Integration by parts
- Some important integrals along with the arms
- Integration of rational algebraic functions by using partial fractions
- When the denominator is expressible as a product of distinct linear factors
- When the denominator contains some repeating linear factors
- The denominator contains irreducible quadratic factors
- Integration of some special irrational algebraic functions
We have included all the information regarding CBSE RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8. If you have any queries feel free to ask in the comment section.
FAQs on RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8
Is RD Sharma Solutions for Class 12 Maths Chapter 19 Exercise 19.8 for free?
Yes, You can get RD Sharma Solutions Class 12 Maths Chapter 19 Exercise 19.8 for free.
Where can I download RD Sharma Solutions Class 12 Chapter 19 Exercise 19.8 free PDF?
You can download RD Sharma Solutions Class 12 Chapter 19 Exercise 19.8 free PDF from the above article.
Are indefinite integrals and Antiderivatives the same?
An antiderivative of a function f(x) is a function whose derivative is equal to f(x). An indefinite integral is an integral written without terminals; it simply asks us to find a general antiderivative of the integrand.