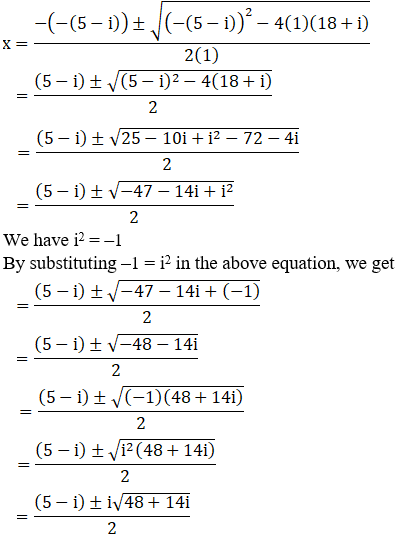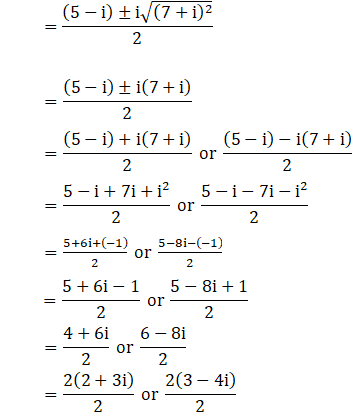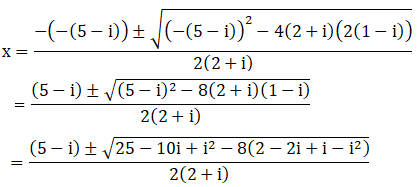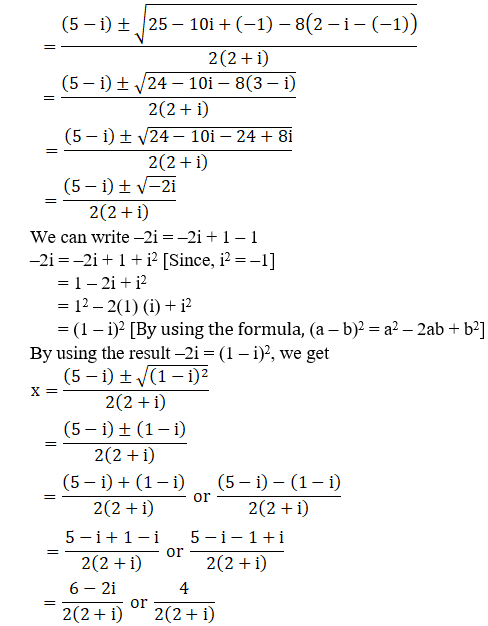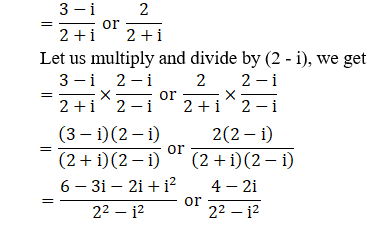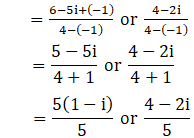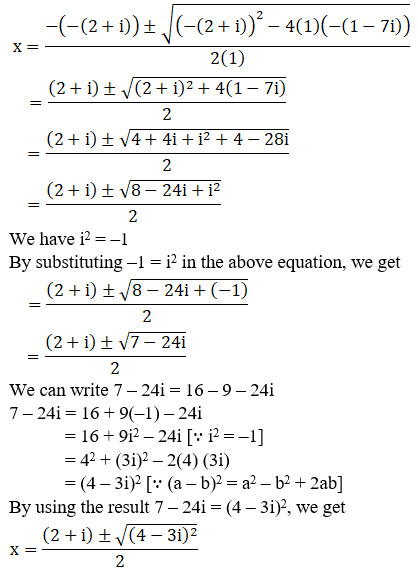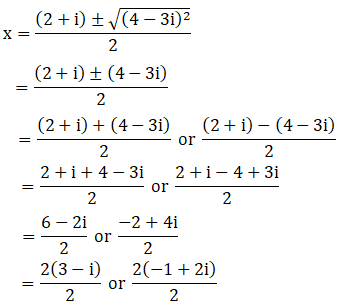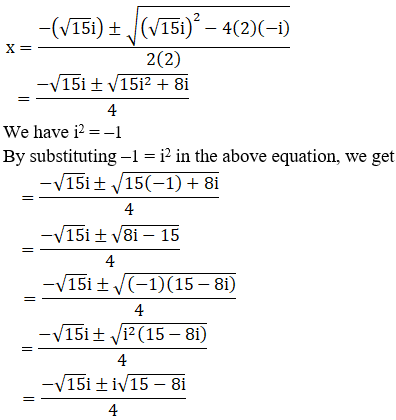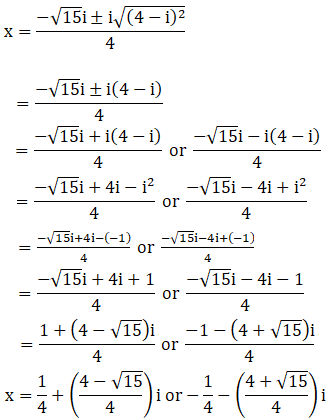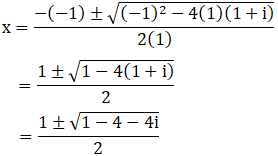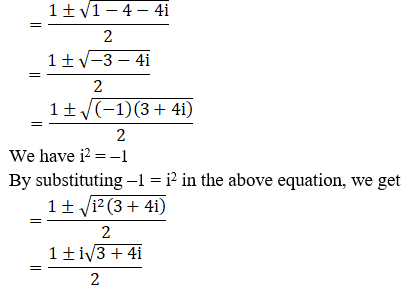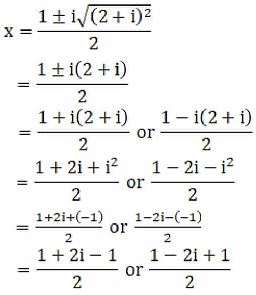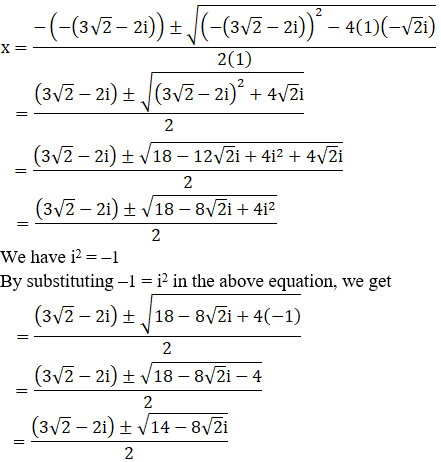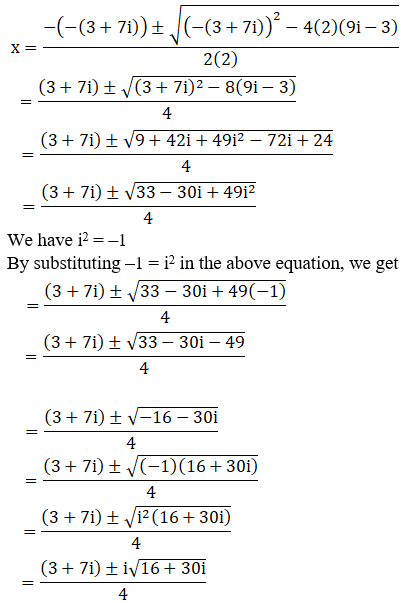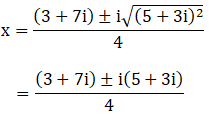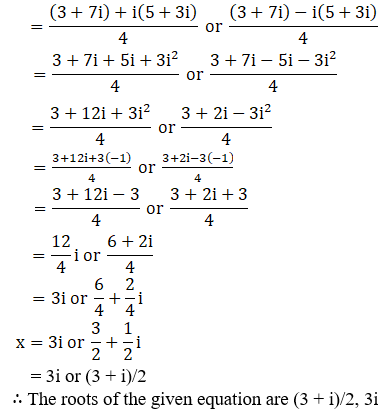RD Sharma Class 11 Solutions Chapter 14 Exercise 14.2 (Updated for 2024)

RD Sharma Solutions Class 11 Maths Chapter 14 Exercise 14.2: You can clear your basics and doubts with the RD Sharma Solutions Class 11 Maths. All the solutions designed by the subject matter experts are as per the current CBSE Syllabus. Go and download the Free PDF of RD Sharma Solutions Class 11 Maths Chapter 14 Exercise 14.2. 

Download RD Sharma Solutions Class 11 Maths Chapter 14 Exercise 14.2 PDF:

RD Sharma Solutions Class 11 Maths Chapter 14 Exercise 14.2

Access answers of RD Sharma Solutions for Class 11 Maths Chapter 14 Exercise 14.2

1. Solving the following quadratic equations by factorization method:

(i) x² + 10ix – 21 = 0

(ii) x² + (1 – 2i)x – 2i = 0

(iii) x² – (2√3 + 3i) x + 6√3i = 0

(iv) 6x² – 17ix – 12 = 0

Solution:

(i) x² + 10ix – 21 = 0

Given: x² + 10ix – 21 = 0

x² + 10ix – 21 × 1 = 0

We know, i² = –1 ⇒ 1 = –i²

By substituting 1 = –i² in the above equation, we get

x² + 10ix – 21(–i²) = 0

x² + 10ix + 21i² = 0

x² + 3ix + 7ix + 21i² = 0

x(x + 3i) + 7i(x + 3i) = 0

(x + 3i) (x + 7i) = 0

x + 3i = 0 or x + 7i = 0

x = –3i or –7i

∴ The roots of the given equation are –3i, –7i

(ii) x² + (1 – 2i)x – 2i = 0

Given: x² + (1 – 2i)x – 2i = 0

x² + x – 2ix – 2i = 0

x(x + 1) – 2i(x + 1) = 0

(x + 1) (x – 2i) = 0

x + 1 = 0 or x – 2i = 0

x = –1 or 2i

∴ The roots of the given equation are –1, 2i

(iii) x² – (2√3 + 3i) x + 6√3i = 0

Given: x² – (2√3 + 3i) x + 6√3i = 0

x² – (2√3x + 3ix) + 6√3i = 0

x² – 2√3x – 3ix + 6√3i = 0

x(x – 2√3) – 3i(x – 2√3) = 0

(x – 2√3) (x – 3i) = 0

(x – 2√3) = 0 or (x – 3i) = 0

x = 2√3 or x = 3i

∴ The roots of the given equation are 2√3, 3i

(iv) 6x² – 17ix – 12 = 0

Given: 6x² – 17ix – 12 = 0

6x² – 17ix – 12 × 1 = 0

We know, i² = –1 ⇒ 1 = –i²

By substituting 1 = –i² in the above equation, we get

6x² – 17ix – 12(–i²) = 0

6x² – 17ix + 12i² = 0

6x² – 9ix – 8ix + 12i² = 0

3x(2x – 3i) – 4i(2x – 3i) = 0

(2x – 3i) (3x – 4i) = 0

2x – 3i = 0 or 3x – 4i = 0

2x = 3i or 3x = 4i

x = 3i/2 or x = 4i/3

∴ The roots of the given equation are 3i/2, 4i/3

2. Solve the following quadratic equations:

(i) x² – (3√2 + 2i) x + 6√2i = 0

(ii) x² – (5 – i) x + (18 + i) = 0

(iii) (2 + i)x² – (5- i)x + 2 (1 – i) = 0

(iv) x² – (2 + i)x – (1 – 7i) = 0

(v) ix² – 4x – 4i = 0

(vi) x² + 4ix – 4 = 0

(vii) 2x² + √15ix – i = 0 

(viii) x² – x + (1 + i) = 0

(ix) ix² – x + 12i = 0

(x) x² – (3√2 – 2i)x – √2i = 0

(xi) x² – (√2 + i)x + √2i = 0

(xii) 2x² – (3 + 7i)x + (9i – 3) = 0

Solution:

(i) x² – (3√2 + 2i) x + 6√2i = 0

Given: x² – (3√2 + 2i) x + 6√2i = 0

x² – (3√2x + 2ix) + 6√2i = 0

x² – 3√2x – 2ix + 6√2i = 0

x(x – 3√2) – 2i(x – 3√2) = 0

(x – 3√2) (x – 2i) = 0

(x – 3√2) = 0 or (x – 2i) = 0

x = 3√2 or x = 2i

∴ The roots of the given equation are 3√2, 2i

(ii) x² – (5 – i) x + (18 + i) = 0

Given: x² – (5 – i) x + (18 + i) = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 1, b = -(5-i), c = (18+i)

So,

We can write 48 + 14i = 49 – 1 + 14i

So,

48 + 14i = 49 + i² + 14i [∵ i² = –1]

= 7² + i² + 2(7)(i)

= (7 + i)² [Since, (a + b)² = a² + b² + 2ab]

By using the result 48 + 14i = (7 + i) ², we get

x = 2 + 3i or 3 – 4i

∴ The roots of the given equation are 3 – 4i, 2 + 3i

(iii) (2 + i)x² – (5- i)x + 2 (1 – i) = 0

Given: (2 + i)x² – (5- i)x + 2 (1 – i) = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = (2+i), b = -(5-i), c = 2(1-i)

So,

We have i² = –1

By substituting –1 = i² in the above equation, we get

x = (1 – i) or 4/5 – 2i/5

∴ The roots of the given equation are (1 – i), 4/5 – 2i/5

(iv) x² – (2 + i)x – (1 – 7i) = 0

Given: x² – (2 + i)x – (1 – 7i) = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 1, b = -(2+i), c = -(1-7i)

So,

We can write 7 – 24i = 16 – 9 – 24i

7 – 24i = 16 + 9(–1) – 24i

= 16 + 9i² – 24i [∵ i² = –1]

= 4² + (3i)² – 2(4) (3i)

= (4 – 3i)² [∵ (a – b)² = a² – b² + 2ab]

By using the result 7 – 24i = (4 – 3i)², we get

x = 3 – i or -1 + 2i

∴ The roots of the given equation are (-1 + 2i), (3 – i)

(v) ix² – 4x – 4i = 0

Given: ix² – 4x – 4i = 0

ix² + 4x(–1) – 4i = 0 [We know, i² = –1]

So by substituting –1 = i² in the above equation, we get

ix² + 4xi² – 4i = 0

i(x² + 4ix – 4) = 0

x² + 4ix – 4 = 0

x² + 4ix + 4(–1) = 0

x² + 4ix + 4i² = 0 [Since, i² = –1]

x² + 2ix + 2ix + 4i² = 0

x(x + 2i) + 2i(x + 2i) = 0

(x + 2i) (x + 2i) = 0

(x + 2i)² = 0

x + 2i = 0

x = –2i, -2i

∴ The roots of the given equation are –2i, –2i

(vi) x² + 4ix – 4 = 0

Given: x² + 4ix – 4 = 0

x² + 4ix + 4(–1) = 0 [We know, i² = –1]

So by substituting –1 = i² in the above equation, we get

x² + 4ix + 4i² = 0

x² + 2ix + 2ix + 4i² = 0

x(x + 2i) + 2i(x + 2i) = 0

(x + 2i) (x + 2i) = 0

(x + 2i)² = 0

x + 2i = 0

x = –2i, -2i

∴ The roots of the given equation are –2i, –2i

(vii) 2x² + √15ix – i = 0 

Given: 2x² + √15ix – i = 0 

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 2, b = √15i, c = -i

So,

We can write 15 – 8i = 16 – 1 – 8i

15 – 8i = 16 + (–1) – 8i

= 16 + i² – 8i [∵ i² = –1]

= 4² + (i)² – 2(4)(i)

= (4 – i)² [Since, (a – b)² = a² – b² + 2ab]

By using the result 15 – 8i = (4 – i)², we get

∴ The roots of the given equation are [1+ (4 – √15)i/4] , [-1 -(4 + √15)i/4]

(viii) x² – x + (1 + i) = 0

Given: x² – x + (1 + i) = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 1, b = -1, c = (1+i)

So,

We can write 3 + 4i = 4 – 1 + 4i

3 + 4i = 4 + i² + 4i [∵ i² = –1]

= 2² + i² + 2(2) (i)

= (2 + i)² [Since, (a + b)² = a² + b² + 2ab]

By using the result 3 + 4i = (2 + i)², we get

x = 2i/2 or (2 – 2i)/2

x = i or 2(1-i)/2

x = i or (1 – i)

∴ The roots of the given equation are (1-i), i

(ix) ix² – x + 12i = 0

Given: ix² – x + 12i = 0

ix² + x(–1) + 12i = 0 [We know, i² = –1]

so by substituting –1 = i² in the above equation, we get

ix² + xi² + 12i = 0

i(x² + ix + 12) = 0

x² + ix + 12 = 0

x² + ix – 12(–1) = 0

x² + ix – 12i² = 0 [Since, i² = –1]

x² – 3ix + 4ix – 12i² = 0

x(x – 3i) + 4i(x – 3i) = 0

(x – 3i) (x + 4i) = 0

x – 3i = 0 or x + 4i = 0

x = 3i or –4i

∴ The roots of the given equation are -4i, 3i

(x) x² – (3√2 – 2i)x – √2i = 0

Given: x² – (3√2 – 2i)x – √2i = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 1, b = -(3√2 – 2i), c = –√2i

So,

(xi) x² – (√2 + i)x + √2i = 0

Given: x² – (√2 + i)x + √2i = 0

x² – (√2x + ix) + √2i = 0

x² – √2x – ix + √2i = 0

x(x – √2) – i(x – √2) = 0

(x – √2) (x – i) = 0

(x – √2) = 0 or (x – i) = 0

x = √2 or x = i

∴ The roots of the given equation are i, √2

(xii) 2x² – (3 + 7i)x + (9i – 3) = 0

Given: 2x² – (3 + 7i)x + (9i – 3) = 0

We shall apply the discriminant rule,

Where, x = (-b ±√(b² – 4ac))/2a

Here, a = 2, b = -(3 + 7i), c = (9i – 3)

So,

We can write 16 + 30i = 25 – 9 + 30i

16 + 30i = 25 + 9(–1) + 30i

= 25 + 9i² + 30i [∵ i² = –1]

= 5² + (3i)² + 2(5)(3i)

= (5 + 3i)² [∵ (a + b)² = a² + b² + 2ab]

By using the result 16 + 30i = (5 + 3i)², we get

This is the complete blog of RD Sharma Solutions for Class 11 Maths Chapter 14 Exercise 14.2. To Know more about the CBSE Class 11 Maths exam, ask in the comments.

FAQs of  RD Sharma Solutions for Class 11 Maths Chapter 14 Exercise 14.2