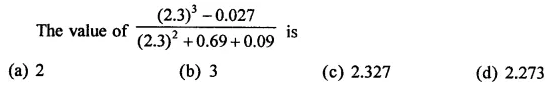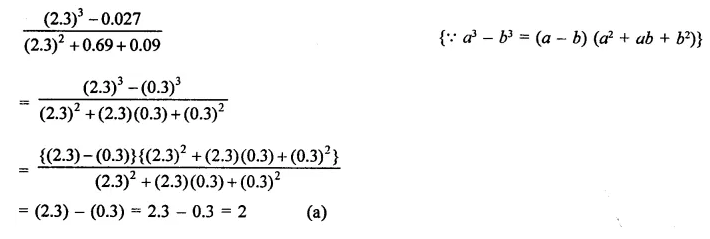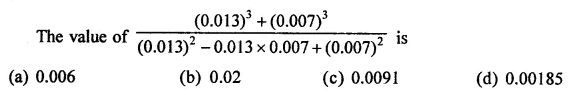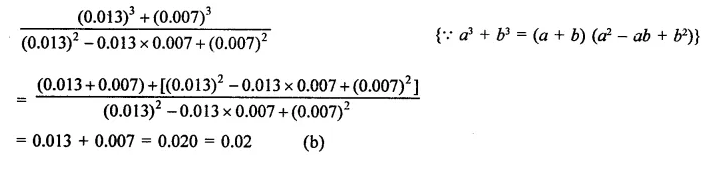RD Sharma Class 9 Solutions: Complete Guide [2026]

Read more: RD Sharma — Complete Guide

RD Sharma Class 9 Solutions Chapter 5 MCQS: Subject matter experts have designed these easy-to-understand solutions for you in the RD Sharma Solutions Class 9 Maths. All the solutions are as per the current CBSE Syllabus 2026. You can clear your concepts and score good marks in your Maths exam with RD Sharma Class 9 Solutions Chapter 5 MCQS.

Algebra ke factorization topic mein mastery pane ke liye, ye MCQs bilkul perfect hain. Chapter 5 mein algebraic expressions ko factorize karna sikhaya gaya hai jo Class 9 students ke liye bohot important hai. These questions help you understand different factorization techniques jaise common factors, grouping method, aur special identities ka use.

Access answers of RD Sharma Class 9 Solutions Chapter 5 MCQS

Yahan par aapko complete solutions milenge jo step-by-step explain kiye gaye hain. Har question ka detailed solution diya gaya hai taki aap concept clear kar sako. Ye MCQs specially designed hain CBSE board exam pattern ke according.

Mark the correct alternative in each of the following:
Question 1.
The factors of x³ – x²y -xy² + y³ are
(a) (x + y) (x² -xy + y²)
(b) (x+y)(x² + xy + y²)
(c) (x + y)² (x – y)
(d) (x – y)² (x + y)
Solution:
x³ – x²y – xy² + y³
= x³ + y³ – x²y – xy²
= (x + y) (x² -xy + y²)- xy(x + y)
= (x + y) (x² – xy + y² – xy)
= (x + y) (x² – 2xy + y²)
= (x + y) (x – y)² (d)

Is question mein hum grouping method use kar rahe hain. Pehle terms ko rearrange kiya, phir common factors nikale. Ye technique bohot useful hai complex expressions ko factorize karne ke liye.

Question 2.
The factors of x³ – 1 +y³ + 3xy are
(a) (x – 1 + y) (x² + 1 + y² + x + y – xy)
(b) (x + y + 1) (x² + y² + 1- xy – x – y)
(c) (x – 1 + y) (x² – 1 – y² + x + y + xy)
(d) 3(x + y – 1) (x² + y² – 1)
Solution:
x³ – 1 + y³ + 3xy
= (x)³ + (-1)³ + (y)³ – 3 x x x (-1) x y
= (x – 1 + y) (x² + 1 + y² + x + y – xy)
= (x- 1 + y) (x²+ 1 + y² + x + y – xy) (a)

Yahan sum of cubes identity ka use kiya gaya hai: a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca). Ye formula yaad rakhna zaroori hai.

Question 3.
The factors of 8a³ + b³ – 6ab + 1 are
(a) (2a + b – 1) (4a² + b² + 1 – 3ab – 2a)
(b) (2a – b + 1) (4a² + b² – 4ab + 1 – 2a + b)
(c) (2a + b+1) (4a² + b² + 1 – 2ab – b – 2a)
(d) (2a – 1 + b)(4a² + 1 – 4a – b – 2ab)
Solution:
8a³ + b³ – 6ab + 1
= (2a)³ + (b)³ + (1)³ – 3 x 2a x b x 1
= (2a + b + 1) [(2a)² + b²+1-2a x b- b x 1 – 1 x 2a]
= (2a + b + 1) (4a² + b²+1-2ab-b- 2a) (c)

Is type ke questions mein pehle check karna chahiye ki kya expression sum of cubes ke form mein convert ho sakti hai. Agar coefficient different hain to unhe perfect cubes banane ki koshish karni chahiye.

Question 4.
(x + y)³ – (x – v)³ can be factorized as
(a) 2y (3x² + y²)
(b) 2x (3x² + y²)
(c) 2y (3y² + x²)
(d) 2x (x² + 3y²)
Solution:
(x + y)³ – (x – y)³
= (x + y -x + y) [(x + y)² + (x +y) (x -y) + (x – y)²]
= 2y(x² + y² + 2xy + x²-y² + x²+y² – 2xy)
= 2y(3x² + y²) (a)

Difference of cubes formula: a³ – b³ = (a – b)(a² + ab + b²). Is question mein a = (x + y) aur b = (x – y) hai.

Question 5.
The expression (a – b)³ + (b – c)³ + (c – a)³ can be factorized as
(a) (a -b) (b- c) (c – a)
(b) 3(a – b) (b – c) (c – a)
(c) -3(a – b) (b – c) (a – a)
(d) (a + b + c) (a² + b² + c² – ab – bc – ca)
Solution:
(a – b)³ + (b – c)³ + (c – a)³
Let a – b = x, b – c = y, c – a = z
∴ x³ + y³ + z³
x+y + z = a- b + b- c + c – a = 0
∴ x³ +y³ + z³ = 3xyz
(a – b)³ + (b – c)³ + (c – a)³
= 3 (a – b) (b – c) (c – a) (b)

Ye special case hai jahan x + y + z = 0 hota hai to x³ + y³ + z³ = 3xyz. Ye identity bohot important hai aur exam mein frequently aati hai.

Question 6.
RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q6.1.png” sizes=”(max-width: 554px) 100vw, 554px” srcset=”https://www.learninsta.com/wp-content/uploads/2018/06/RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q6.1.png 554w, https://www.learninsta.com/wp-content/uploads/2018/06/RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q6.1-300×51.png 300w” alt=”RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q6.1″ width=”554″ height=”94″ />
Solution:

Question 7.
RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q7.1.png” sizes=”(max-width: 576px) 100vw, 576px” srcset=”https://www.learninsta.com/wp-content/uploads/2018/06/RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q7.1.png 576w, https://www.learninsta.com/wp-content/uploads/2018/06/RD-Sharma-Class-9-Solutions-Chapter-5-Factorisation-of-Algebraic-Expressions-MCQS-Q7.1-300×54.png 300w” alt=”RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q7.1″ width=”576″ height=”103″ />
Solution:

Question 8.
The factors of a² – 1 – 2x – x² are
(a) (a – x + 1) (a – x – 1)
(b) (a + x – 1) (a – x + 1)
(c) (a + x + 1) (a – x – 1)
(d) none of these
Solution:
a² – 1- 2x – x²
⇒ a² – (1 + 2x + x²)
= (a)² – (1 + x)²
= (a + 1 + x) (a – 1 – x) (c)

Yahan difference of squares formula use kiya gaya hai: a² – b² = (a + b)(a – b). Pehle expression ko perfect square banaya, phir formula apply kiya.

Question 9.
The factors of x⁴ + x² + 25 are
(a) (x² + 3x + 5) (x² – 3x + 5)
(b) (x² + 3x + 5) (x² + 3x – 5)
(c) (x² + x + 5) (x² – x + 5)
(d) none of these
Solution:
x⁴ + x² + 25 = x⁴ + 25 +x²
= (x²)² + (5)² + 2 x x² x 5- 9x²
= (x² + 5)² – (3x)²
= (x² + 5 + 3x) (x² + 5 – 3x)
= (x² + 3x + 5) (x² – 3x + 5) (a)

Is question mein smart technique use ki gayi hai. Expression ko complete square banane ke liye middle term add aur subtract kiya, phir difference of squares apply kiya.

Question 10.
The factors of x² + 4y² + 4y – 4xy – 2x – 8 are
(a) (x – 2y – 4) (x – 2y + 2)
(b) (x – y + 2) (x – 4y – 4)
(c) (x + 2y – 4) (x + 2y + 2)
(d) none of these
Solution:
x² + 4y² + 4y – 4xy – 2x – 8
⇒ x² + 4y + 4y – 4xy – 2x – 8
= (x)² + (2y)²– 2 x x x 2y + 4y-2x-8
= (x – 2y)² – (2x – 4y) – 8
= (x – 2y)² – 2 (x – 2y) – 8
Let x – 2y = a, then
a²– 2a – 8 = a²– 4a + 2a – 8
= a(a – 4) + 2(a – 4)
= (a-4) (a + 2)
= (x² -2y-4) (x² -2y + 2) (a)

Substitution method ka use karke complex expressions ko simple bana sakte hain. Yahan x – 2y = a rakha to quadratic equation mil gaya.

Question 11.
The factors of x³ – 7x + 6 are
(a) x(x – 6) (x – 1)
(b) (x² – 6) (x – 1)
(c) (x + 1) (x + 2) (x – 3)
(d) (x – 1) (x + 3) (x – 2)
Solution:
x³ -7x + 6= x³-1-7x + 7
= (x – 1) (x² + x + 1) – 7(x – 1)
= (x – 1) (x² + x + 1 – 7)
= (x – 1) (x² + x – 6)
= (x – 1) [x² + 3x – 2x – 6]
= (x – 1) [x(x + 3) – 2(x + 3)]
= (x – 1) (x+ 3) (x – 2) (d)

Cubic expressions ko factorize karne ke liye rational root theorem use kar sakte hain. Pehle possible rational roots check karo, phir synthetic division ya grouping method apply karo.

Question 12.
The expression x⁴ + 4 can be factorized as
(a) (x² + 2x + 2) (x² – 2x + 2)
(b) (x² + 2x + 2) (x² + 2x – 2)
(c) (x² – 2x – 2) (x² – 2x + 2)
(d) (x² + 2) (x² – 2)
Solution:
x⁴ + 4 = x⁴ + 4 + 4x² – 4x² (Adding and subtracting 4x²)
= (x²)² + (2)² + 2 x x² x 2 – (2x)²
= (x² + 2)² – (2x)²
= (x² + 2 + 2x) (x² + 2 – 2x) {∵ a² – b² = (a + b) (a – b)}
= (x² + 2x + 2) (x² – 2x + 2) (a)

Sophie Germain identity ka use kiya gaya hai: a⁴ + 4b⁴ = (a² + 2ab + 2b²)(a² – 2ab + 2b²). Ye advanced factorization technique hai.

Question 13.
If 3x = a + b + c, then the value of (x – a)³ + (x – bf + (x – cf – 3(x – a) (x – b) (x – c) is
(a) a + b + c
(b) (a – b) {b – c) (c – a)
(c) 0
(d) none of these
Solution:
3x = a + b + c .
⇒ 3x-a-b-c = 0
Now, (x – a)³+ (x – b)³ + (x – c)³ – 3(x – a) (x -b) (x – c)
= {(x – a) + (x – b) + (x – c)} {(x – a)² + (x – b)² + (x – c)² – (x – a) (x – b) (x – b) (x – c) – (x – c) (x – a)}
= (x – a + x – b + x – c) {(x – a)² + (x – b)² + (x – c)² – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= (3x – a – b -c) {(x – a)² + (x -b)²+ (x – c)² – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
But 3x-a-b-c = 0, then
= 0 x {(x – a)² + (x – b)² + (x – c)² – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= 0 (c)

Ye question sum of cubes identity aur given condition ka clever use dikhata hai. Jab sum zero hota hai to expression simplify ho jata hai.

Question 14.
If (x + y)³ – (x – y)³ – 6y(x² – y²) = ky², then k =
(a) 1
(b) 2
(c) 4
(d) 8
Solution:
(x + y)³ – (x – y)³ – 6y(x² – y²) = ky²
LHS = (x + y)³ – (x – y)³ – 3 x (x + y) (x – y) [x + y – x + y]
= (x+y-x + y)³ {∵ a³ – b³ – 3ab (a – b) = a³ – b³}
= (2y)³ = 8y³
Comparing with ky³, k = 8 (d)

Is question mein algebraic manipulation aur identity ka use karke value of k find kiya gaya hai. Coefficient comparison ka method use kiya.

Question 15.
If x³ – 3x² + 3x – 7 = (x + 1) (ax² + bx + c), then a + b + c =
(a) 4
(b) 12
(c) -10
(d) 3
Solution:
x³ – 3x² + 3x + 7 = (x + 1) (ax² + bx + c)
= ax³ + bx² + cx + ax² + bx + c
x³ – 3x² + 3x – 7 = ax³ + (b + a)² + (c + b)x + c
Comparing the coefficient,
a = 1
b + a = -3 ⇒ b+1=-3 ⇒ b = -3-1=-4
c + b = 3 ⇒ c- 4 = 3 ⇒ c = 3 + 4 = 7
a + b + c = 1- 4 + 7 = 8- 4 = 4 (a)

Polynomial division aur coefficient comparison ka method use karke unknown coefficients find kiye gaye hain. Ye technique algebraic equations solve karne mein useful hai.

Chapter 5 Factorization Techniques Overview

RD Sharma Class 9 Chapter 5 mein different types of factorization techniques cover kiye gaye hain jo students ke liye fundamental hain. Ye techniques algebra ki strong foundation banane ke liye zaroori hain.

Main Factorization Methods:

• Common Factor Method: Sabse basic method hai jahan common factors ko bahar nikala jata hai
• Grouping Method: Terms ko groups mein divide karke factorize karte hain
• Difference of Squares: a² – b² = (a+b)(a-b) identity use karte hain
• Perfect Square Trinomials: a² ± 2ab + b² = (a ± b)² form identify karte hain
• Sum and Difference of Cubes: a³ ± b³ ke special formulas use karte hain
• Substitution Method: Complex expressions ko simple variables se replace karte hain

Har method ka apna specific use case hai. Students ko ye samajhna chahiye ki kab kaunsa method apply karna hai. Practice ke saath ye decision making improve hoti hai.

Board Exam Importance and Weightage

CBSE Board Exam 2026 mein factorization ka significant weightage hai. Algebra section mein ye topic 15-20 marks ka contribute karta hai. Direct questions ke alawa, geometry aur coordinate geometry mein bhi factorization techniques use hote hain.

Expected Question Types in Board Exam:

• 2-3 marks ke short answer questions
• 4-5 marks ke long answer questions with multiple parts
• Application based problems jahan factorization use karni padti hai
• Proof based questions where factorization helps in simplification

Students ko CBSE official website regularly check karna chahiye latest updates ke liye. Sample papers aur marking schemes download kar sakte hain preparation ke liye.

Most important exercises for board exam preparation:

• Exercise 5.1: Basic factorization methods
• Exercise 5.3: Advanced identities and applications
• MCQ section: Quick problem solving skills

Difficulty Level Progression

RD Sharma solutions mein difficulty level gradually increase hoti hai jo students ke learning curve ke according designed hai.

Basic Level (Questions 1-5):

Ye questions simple identities aur basic factorization techniques cover karte hain. Students ko pehle ye master karna chahiye before moving to advanced topics. Common mistakes avoid karne ke liye step-by-step approach follow karna important hai.

Moderate Level (Questions 6-10):

Is level mein mixed techniques use karni padti hain. Multiple methods combine karne ke questions aate hain. Substitution method aur algebraic manipulation skills develop hoti hain.

Advanced Level (Questions 11-15):

Complex expressions aur higher degree polynomials ke questions hain. Ye questions competitive exams ke liye bhi useful hain. Critical thinking aur pattern recognition skills develop karte hain.

Tips for Maximum Benefit:

• NCERT concepts pehle clear karo, phir RD Sharma practice karo
• Har method ke liye separate practice sessions rakho
• Mistakes ko note karo aur revise karte raho
• Time management skills develop karo through regular practice

Regular practice se confidence build hoti hai aur exam mein better performance mil sakti hai. Students ko daily practice routine maintain karna chahiye consistent improvement ke liye.

This is the complete blog on RD Sharma Class 9 Solutions Chapter 5 MCQS. To know more about the CBSE Class 9 Maths exam, ask in the comments.

FAQs on RD Sharma Class 9 Solutions Chapter 5 MCQS