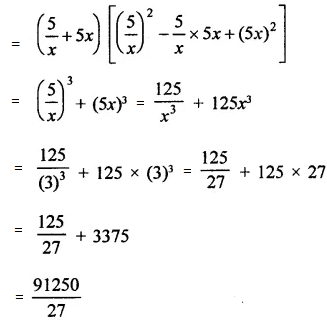RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4 (Updated for 2024)

RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4: You can always clear your doubts and get help in getting good marks in your Class 9 Maths exams with RD Sharma Solutions Class 9 Maths. It is important to understand everything from the core and you can do it by practicing the questions of RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4.  

Download RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4 PDF

RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4

Access answers of RD Sharma Class 9 Solutions Chapter 4 Exercise 4.4

Question 1: Find the following products:

(i) (3x + 2y)(9x² – 6xy + 4y²)

(ii) (4x – 5y)(16x² + 20xy + 25y²)

(iii) (7p⁴ + q)(49p⁸ – 7p⁴q + q²)

(iv) (x/2 + 2y)(x²/4 – xy + 4y²)

(v) (3/x – 5/y)(9/x² + 25/y² + 15/xy)

(vi) (3 + 5/x)(9 – 15/x + 25/x²)

(vii) (2/x + 3x)(4/x² + 9x² – 6)

(viii) (3/x – 2x²)(9/x² + 4x⁴ – 6x)

(ix) (1 – x)(1 + x + x²)

(x) (1 + x)(1 – x + x²)

(xi) (x² – 1)(x⁴ + x² +1)

(xii) (x³ + 1)(x⁶ – x³ + 1)

Solution:

(i) (3x + 2y)(9x² – 6xy + 4y²)

= (3x + 2y)[(3x)² – (3x)(2y) + (2y)²)]

We know, a³ + b³ = (a + b)(a² + b² – ab)

= (3x)³ + (2y) ³

= 27x³ + 8y³

(ii) (4x – 5y)(16x² + 20xy + 25y²)

= (4x – 5y)[(4x)² + (4x)(5y) + (5y)²)]

We know, a³ – b³ = (a – b)(a² + b² + ab)

= (4x)³ – (5y) ³

= 64x³ – 125y³

(iii) (7p⁴ + q)(49p⁸ – 7p⁴q + q²)

= (7p⁴ + q)[(7p⁴)² – (7p⁴)(q) + (q)²)]

We know, a³ + b³ = (a + b)(a² + b² – ab)

= (7p⁴)³ + (q) ³

= 343 p¹² + q³

(iv) (x/2 + 2y)(x²/4 – xy + 4y²)

We know, a³ – b³ = (a – b)(a² + b² + ab)

(x/2 + 2y)(x²/4 – xy + 4y²)

(v) (3/x – 5/y)(9/x² + 25/y² + 15/xy)

[Using a³ – b³ = (a – b)(a² + b² + ab) ]

(vi) (3 + 5/x)(9 – 15/x + 25/x²)

[Using: a³ + b³ = (a + b)(a² + b² – ab)]

(vii) (2/x + 3x)(4/x² + 9x² – 6)

[Using: a³ + b³ = (a + b)(a² + b² – ab)]

(viii) (3/x – 2x²)(9/x² + 4x⁴ – 6x)

[Using : a³ – b³ = (a – b)(a² + b² + ab)]

(ix) (1 – x)(1 + x + x²)

And we know, a³ – b³ = (a – b)(a² + b² + ab)

(1 – x)(1 + x + x²) can be written as

(1 – x)[(1² + (1)(x)+ x²)]

= (1)³ – (x)³

= 1 – x³

(x) (1 + x)(1 – x + x²)

And we know, a³ + b³ = (a + b)(a² + b² – ab)]

(1 + x)(1 – x + x²) can be written as,

(1 + x)[(1² – (1)(x) + x²)]

= (1)³ + (x) ³

= 1 + x³

(xi) (x² – 1)(x⁴ + x² +1) can be written as,

(x² – 1)[(x²)² – 1² + (x²)(1)]

= (x²)³ – 1³

= x⁶ – 1

[using a³ – b³ = (a – b)(a² + b² + ab) ]

(xii) (x³ + 1)(x⁶ – x³ + 1) can be written as,

(x³ + 1)[(x³)² – (x³)(1) + 1²]

= (x³) ³ + 1³

= x⁹ + 1

[using a³ + b³ = (a + b)(a² + b² – ab) ]

Question 2: If x = 3 and y = -1, find the values of each of the following using in identity:

(i) (9y² – 4x²)(81y⁴ + 36x²y² + 16x⁴)

(ii) (3/x – x/3)(x² /9 + 9/x² + 1)

(iii) (x/7 + y/3)(x²/49 + y²/9 – xy/21)

(iv) (x/4 – y/3)(x²/16 + xy/12 + y²/9)
(v) (5/x + 5x)(25/x² – 25 + 25x²)

Solution:

(i) (9y² – 4x²)(81y⁴ + 36x²y² + 16x⁴)

= (9y² – 4x²) [(9y² ) ² + 9y² x 4x² + (4x²) ² ]

= (9y² ) ³ – (4x²)³

= 729 y⁶ – 64 x⁶

Put x = 3 and y = -1

= 729 – 46656

= – 45927

(ii) Put x = 3 and y = -1

(3/x – x/3)(x² /9 + 9/x² + 1)

(iii) Put x = 3 and y = -1

(x/7 + y/3)(x²/49 + y²/9 – xy/21)

(iv) Put x = 3 and y = -1

(x/4 – y/3)(x²/16 + xy/12 + y²/9)

(v) Put x = 3 and y = -1

(5/x + 5x)(25/x² – 25 + 25x²)

Question 3: If a + b = 10 and ab = 16, find the value of a² – ab + b² and a² + ab + b².

Solution:

a + b = 10, ab = 16

Squaring, a + b = 10, both sides

(a + b)² = (10)²

a² + b² + 2ab = 100

a² + b² + 2 x 16 = 100

a² + b² + 32 = 100

a² + b² = 100 – 32 = 68

a² + b² = 68

Again, a² – ab + b² = a² + b² – ab = 68 – 16 = 52 and

a² + ab + b² = a² + b² + ab = 68 + 16 = 84

Question 4: If a + b = 8 and ab = 6, find the value of a³ + b³.

Solution:

a + b = 8, ab = 6

Cubing, a + b = 8, both sides, we get

(a + b)³ = (8)³

a³ + b³ + 3ab(a + b) = 512

a³ + b³ + 3 x 6 x 8 = 512

a³ + b³ + 144 = 512

a³ + b³ = 512 – 144 = 368

a³ + b³ = 368

This is the complete blog of RD Sharma Solutions Class 9 Maths Chapter 4 Exercise 4.4. To know more about the CBSE Class 9 Maths exam, ask in the comments. 

FAQs on RD Sharma Solutions Class 9 Maths Chapter 4 Exercise 4.4