RD Sharma Class 9 Solutions Maths Chapter 24 MCQS (Updated for 2024)

RD Sharma Class 9 Solutions Chapter 24 MCQS: RD Sharma Class 9 Solutions Maths Chapter 24 MCQS PDF files are freely available. This PDF was created by our team of experts. These solutions are very useful for the 9th-grade exams. You can see these solutions in detail when studying for the exam.

• RD Sharma Class 9 Maths Solutions

Access RD Sharma Class 9 Solutions Chapter 24 MCQS

Question 1.
Which one of the following is not a measure of central value?
(a) Mean
(b) Range
(c) Median
(d) Mode
Solution:
Range (b)

Question 2.
The mean of n observations is X¯¯¯¯ . If k is added to each observation, then the new mean is
(a) X¯¯¯¯
(b) X¯¯¯¯ + k
(c) X¯¯¯¯ – k
(d) kX¯¯¯¯
Solution:
Mean of n observation = X¯¯¯¯
By adding k to each observation the new mean will be X¯¯¯¯ + k (b)

Question 3.
The mean of n observations is X¯¯¯¯ . If each observation is multiplied by k, the mean of new observations is
(a) kX¯¯¯¯
(b) X¯¯¯¯¯k
(c) X¯¯¯¯ + k
(d) X¯¯¯¯ – k
Solution:
Mean of n observations = X¯¯¯¯
By multiplying each observation by k,
the new mean = kX¯¯¯¯ (a)

Question 4.
The mean of a set of seven numbers is 81. If one of the numbers is discarded, the mean of the remaining numbers is 78. The value of a discarded number is
(a) 98
(b) 99
(c) 100
(d) 101
Solution:
The mean of 7 numbers = 81
Total = 7 x 81 = 567
By discarding one number, the mean of the remaining 7 – 1 = 6 numbers = 78
Total = 6 x 78 = 468
Discarded number = 567 – 468 = 99 (b)

Question 5.
For which set of numbers do the mean, median and mode all have the same value?
(a) 2, 2, 2, 2, 4
(b) 1, 3, 3, 3, 5
(c) 1, 1, 2, 5, 6
(d) 1, 1, 1, 2, 5
Solution:
a) In set 2, 2, 2, 2, 4

Mode = 3 as it comes in maximum times
This set has the mean, median, and mode same (b)

Question 6.
For the set of numbers 2, 2, 4, 5, and 12, which of the following statements is true?
(a) Mean = Median
(b) Mean > Mode
(c) Mean < Mode
(d) Mode = Median
Solution:
The given set is 2, 2, 4, 5, 12

Question 6.
For the set of numbers 2, 2, 4, 5, and 12, which of the following statements is true?
(a) Mean = Median
(b) Mean > Mode
(c) Mean < Mode
(d) Mode = Median
Solution:
The given set is 2, 2, 4, 5, 12

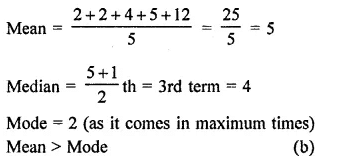
Question 7.
If the arithmetic mean of 7, 5, 13, x and 9 is 10, then the value of x is
(a) 10
(b) 12
(c) 14
(d) 16
Solution:
The arithmetic mean of 7, 5, 13, x, 9 is 10

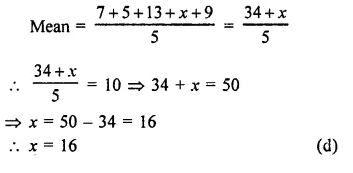
Question 8.
If the mean of five observations x, x + 2, x + 4, x + 6, x + 8, is 11, then the mean of first three observations is
(a) 9
(b) 11
(c) 13
(d) none of these
Solution:
Mean = 11
But mean of x, x + 2, x + 4, x+ 6, x + 8

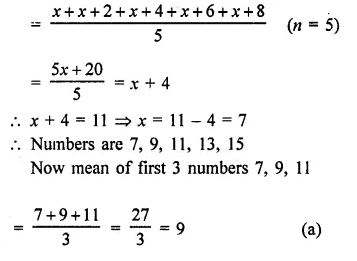
Question 9.
Mode is
(a) least frequent value
(b) middlemost value
(c) most frequent value
(d) none of these
Solution:
Mode is the most frequent value (c)

Question 10.
The following is the data of wages per day: 5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8 The mode of the data is
(a) 7
(b) 5
(c) 8
(d) 10
Solution:
Wages per day
5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8
=> 4, 5, 5, 5, 5, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10
Here 8 comes in the maximum times
Mode = 8 (c)

Question 11.
The median of the following data :
is,
(a) 0
(b) -1.5
(c) 2
(d) 3.5
Solution:
Arranging in ascending order,
-3, -3, -1, 0, 2, 2, 2, 5, 5, 5, 5, 6, 6, 6

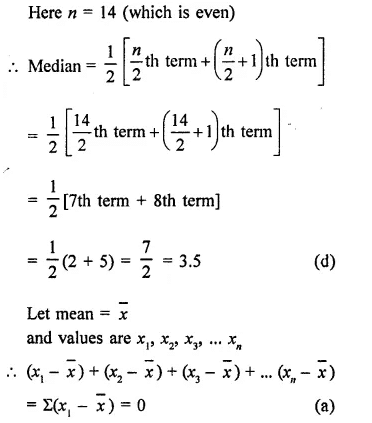
Question 12.
The algebraic sum of the deviations of a set of n values from their mean is
(a) 0
(b) n – 1
(c) n
(d) n + 1
Solution:
The algebraic sum of deviation of a set of n values from that mean

Question 13.
A, B, C are three sets of values of X:
A : 2, 3, 7, 1, 3, 2, 3
B: 7, 5, 9, 12, 5, 3, 8
C: 4, 4, 11, 7 ,2, 3, 4
Which one of the following statements is
correct?
(a) Mean of A = Mode of C
(b) Mean of C = Median of B
(c) Median of B = Mode of A
(d) Mean, Median, and Mode of A are equal.
Solution:
Arranging the sets in ascending order
A{2, 3, 7, 1,3,2,3)
= {1, 2, 2, 3, 3, 3, 7)
B = {7, 5, 9, 12, 5, 3, 8)
= {3, 5, 5, 7, 8, 9, 12)
C = {4, 4, 11,7,2,3,4)
= {2, 3, 4, 4, 4, 7, 11)

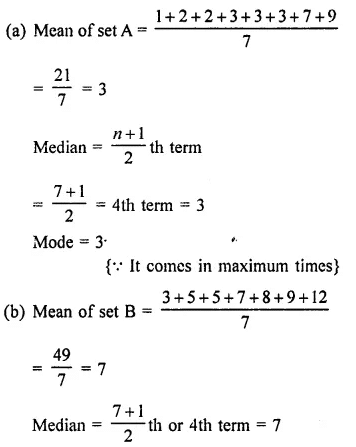
Mode = 5 {as it comes max times}
(c) Mean of set C = 2+3+4+4+4+7+117
= 357 = 5
Median = 7+12 th =82 =4th term = 4
Mode =4 {as it comes max times}
In set A,mean = median = mode = 3 (d)

Question 14.
The empirical relation between mean, mode and median is
(a) Mode = 3 Median — 2 Mean
(b) Mode 2 Median — 3 Mean
(c) Median 3 Mode — 2 Mean
(d) Mean = 3 Median —2 Mode
Solution:
The empirical relations between mean, mode
and median is
Mode = 3 Median — 2 Mean (a)

Question 15.
The mean of a, b, c, d, and e is 28. If the mean of a, c, and e is 24, what is the mean of b and d?
(a) 31
(b) 32
(c) 33
(d) 34
Solution:
Mean of a, b, c, d and e = 28
Total of a, b, c, d and e = 28 x 5 = 140
Mean of a, c and e is = 24
Total of a, c, e = 24 x 3 = 72
Total of b and d = 140 – 72 = 68
Mean = 682 = 34 (d)

We have included all the information regarding CBSE RD Sharma Class 9 Solutions Chapter 24 MCQS. If you have any queries feel free to ask in the comment section. 

FAQ: RD Sharma Class 9 Solutions Chapter 24 MCQS