RD Sharma Class 10 Solutions Chapter 1 VSAQs (Updated for 2024)

RD Sharma Class 10 Solutions Chapter 1 VSAQs: If you’re facing any difficulty in understanding a question from this exercise, the RD Sharma Solutions Class 10 is the perfect resource for you. Students can download RD Sharma Class 10 Solutions Chapter 1 VSAQS Free PDF from the below-mentioned link.

Access RD Sharma Class 10 Solutions Chapter 1 VSAQs

Question 1.
State Euclid’s division lemma.
Solution:
Euclid’s division lemma:
Let a and b be any two positive integers, then there exist unique integers q and r such that
a = bq + r, 0 ≤ r < b
If b\a, then r = 0, otherwise x. satisfies the stronger inequality 0 < r < b.

Question 2.
State Fundamental Theorem of Arithmetic.
Solution:
Fundamental Theorem of Arithmetics :
Every composite number can be expressed (factorized) as a product of primes and this factorization is unique except for the order in which the prime factors occur.

Question 3.
Write 98 as a product of its prime factors.
Solution: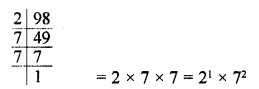

Question 4.
Write the exponent of 2 in the prime factorization of 144.
Solution: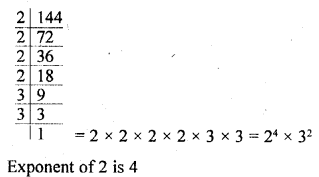

Question 5.
Write the sum of the exponents of prime factors in the prime factorization of 98
Solution:
98 = 2 x 7 x 7 = 2¹ x 7²
Sum of exponents = 1 + 2 = 3

Question 6.
If the prime factorization of a natural number n is 2³ x 3² x 5² x 7, write the number of consecutive zeros in n.
Solution:
n = 2³ x 3² x 5² x 7
Number of zeros will be 5² x 2² = 10² two zeros

Question 7.
If the product of two numbers is 1080 and their H.C.F. is 30, find their L.C.M.
Solution:
Product of two numbers = 1080
H.C.F. = 30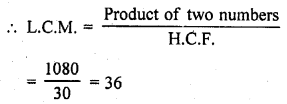

Question 8.
Write the condition to be satisfied by q so that a rational number pq has a terminating decimal expansion. [C.B.S.E. 2008]
Solution:
In the rational number pq, the factorization of denominator q must be in the form of 2^m x 5ⁿ where m and n are non-negative integers.

Question 9.
Write the condition to be satisfied by q so that a rational number pq has a non-terminating decimal expansion.
Solution:
In the rational number pq, the factorization of denominator q, is not in the form of 2^m x 5ⁿ where m and n are non-negative integers.

Question 10.
Complete the missing entries in the following factor tree.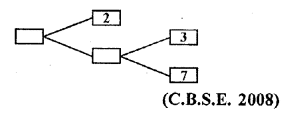

Solution: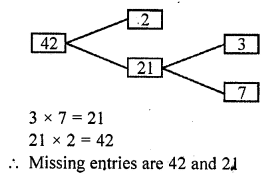

Question 11.
The decimal expression of the rational number 4324×53 will terminate after how many places of decimals. [C.B.S.E. 2009]
Solution:
The denominator of 4324×53 is 24 x 53 which is in the form of 2^m x 5ⁿ where m and n are positive integers
4324×53 has terminating decimals
The decimal expansion of 4324×53 terminates after 4 (the highest power is 4) decimal places

Question 12.
Has the rational number 44125×57×72 of a terminating or a non-terminating decimal representation? [CBSE 2010]
Solution:

Question 13.
Write whether 2√45+3√202√5 on simplification gives a rational or an irrational number. [CBSE 2010]
Solution: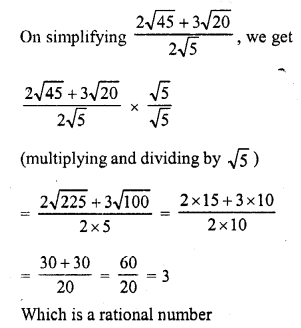

Question 14.
What is an algorithm?
Solution:
Algorithm: An algorithm is a series of well-defined slips that gives a procedure for solving a type of problem.

Question 15.
What is a lemma?
Solution:
A lemma is a proven statement used for proving another statement.

Question 16.
If p and q are two prime numbers, then what is their HCF?
Solution:
If p and q are two primes, then their HCF will be 1 as they have no common factor except 1.

Question 17.
If p and q are two prime numbers, then what is their LCM?
Solution:
If p and q are two primes, their LCM will be their product.

Question 18.
What is the total number of factors of a prime number?
Solution:
The total number of factors of a prime number is 2, first 1 and second the number itself.

Question 19.
What is a composite number?
Solution:
A composite number is a number that can be factorized into more than two factors.

Question 20.
What is the HCF of the smallest composite number and the smallest prime number?
Solution:
We know that 2 is the smallest prime number and 4 is the smallest composite number
HCF of 2 and 4 = 2

Question 21.
HCF of two numbers is always a factor of their LCM (True / False).
Solution:
True.

Question 22.
π is an irrational number (True / False).
Solution:
True as the value of π is neither terminating nor repeating.

Question 23.
The sum of two prime numbers is always a prime number (True / False).
Solution:
False. The sum of two prime numbers can be a composite number
e.g. 3 and 5 are prime numbers but their sum 3 + 5 = 8 is a composite number.

Question 24.
The product of any three consecutive natural numbers is divisible by 6 (True / False).
Solution:
True.

Question 25.
Every even integer is of the form 2m, where m is an integer (True / False).
Solution:
True, as 2m is divisible by 2.

Question 26.
Every odd integer is of the form 2m – 1, where m is an integer (True / False).
Solution:
True, as 2m is an even number but if we subtract 1 from it, it will be an odd number.

Question 27.
The product of two irrational numbers is an irrational number (True / False).
Solution:
False, as it is not always possible for the product of two irrational numbers be also an irrational number, it may be a rational number
for example
√3 x √3 = 3, √7 x √7 = 7

Question 28.
The sum of two irrational numbers is an irrational number (True / False).
Solution:
False, as it is not always possible that the sum of two irrational is also an irrational number, it may be a rational number also.
For example
(2 + √3) + (2 – √3) = 2 + √3 + 2 – √3 = 4

Question 29.
For what value of n, 2ⁿ x 5ⁿ ends in 5.
Solution:
In 2ⁿ x 5ⁿ ,
There is no such value of n, which satisfies the given condition.

Question 30.
If a and b are relatively prime numbers, then what is their HCF?
Solution:
a and b are two prime numbers
Their HCF =1

Question 31.
If a and b are relatively prime numbers, then what is their LCM?
Solution:
a and b are two prime numbers
Their LCM = a x b

Question 32.
Two numbers have 12 as their HCF and 350 as their LCM (True / False).
Solution:
HCF of two numbers = 12
and LCM is 350
False, as the HCF of two numbers is a factor of their LCM and 12 is not a factor of 350.

We have provided complete details of RD Sharma Class 10 Solutions Chapter 1 VSAQS. If you have any queries related to CBSE Class 10, feel free to ask us in the comment section below.

FAQs on RD Sharma Class 10 Solutions Chapter 1 VSAQS